在数学的世界里，椭圆与双曲线是两种基本的曲线形态，它们在几何、物理、工程等领域有着广泛的应用，本文旨在深入探讨椭圆与双曲线的概念、性质、公式及其相互关系，为读者揭示这两类曲线的奥秘。

椭圆的基本概念与性质

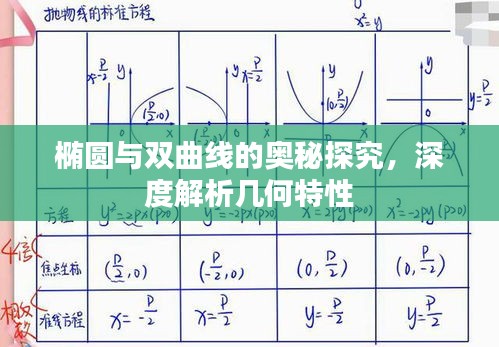
椭圆是平面内到两定点（焦点）的距离之和等于常数的点的轨迹，这两定点称为椭圆的焦点，而连接这两焦点的线段称为焦距，椭圆具有许多重要的性质，如焦点性质、长轴与短轴的性质等，椭圆的标准方程及其推导过程也是研究椭圆的重要内容。

双曲线的基本概念与性质

双曲线是平面内到两定点（焦点）的距离之差的绝对值为常数的点的轨迹，这两定点称为双曲线的焦点，而连接这两焦点的线段称为焦距，双曲线同样具有许多重要的性质，如焦点性质、渐近线性质等，双曲线的标准方程及其推导过程也是研究双曲线的重要内容。

椭圆与双曲线的相互关系

椭圆和双曲线之间存在许多有趣的联系和对比，两者都有焦点和焦距的概念，但焦距与椭圆和双曲线的关系不同，在某些特定情况下，椭圆可以转化为双曲线，反之亦然，这种转化对于理解两者的性质具有重要意义。

专题应用

椭圆和双曲线在各个领域有着广泛的应用，在几何学中，它们是最基本的曲线形态之一，具有许多重要的性质和定理，在物理学中，椭圆和双曲线的运动轨迹常常出现在行星运动、电磁波传播等现象中，在工程领域，椭圆和双曲线的应用更是广泛，如机械零件的截面设计、光学仪器的镜头设计等。

研究方法与公式推导

研究椭圆与双曲线的方法主要包括几何法和解析法，几何法通过直观的图形分析来推导性质与公式，而解析法则是通过代数方程来研究曲线的性质，在公式推导过程中，我们需要掌握基本的概念和定理，如椭圆的焦点公式、双曲线的渐近线公式等，还需要运用微积分等高级数学知识来求解相关问题。

椭圆与双曲线是数学中的基本曲线形态，它们在各个领域有着广泛的应用，通过对这两类曲线的研究，我们可以深入了解曲线的性质、公式及其相互关系，为实际应用提供有力的支持，随着科技的不断发展，椭圆与双曲线的研究将具有更广阔的应用前景和更深入的理论研究。

参考文献

本文参考文献主要包括相关的数学教材、学术论文和研究专著等，通过查阅这些文献，我们可以更深入地了解椭圆与双曲线的相关知识，为本文提供坚实的理论基础和实证支持。